正解・不正解よりもどう考えたのか、が重要です。
今朝、年長息子Z会9月号が終了しました。9月号は最後2ページが小学生準備内容になっています。内容は算数と国語。
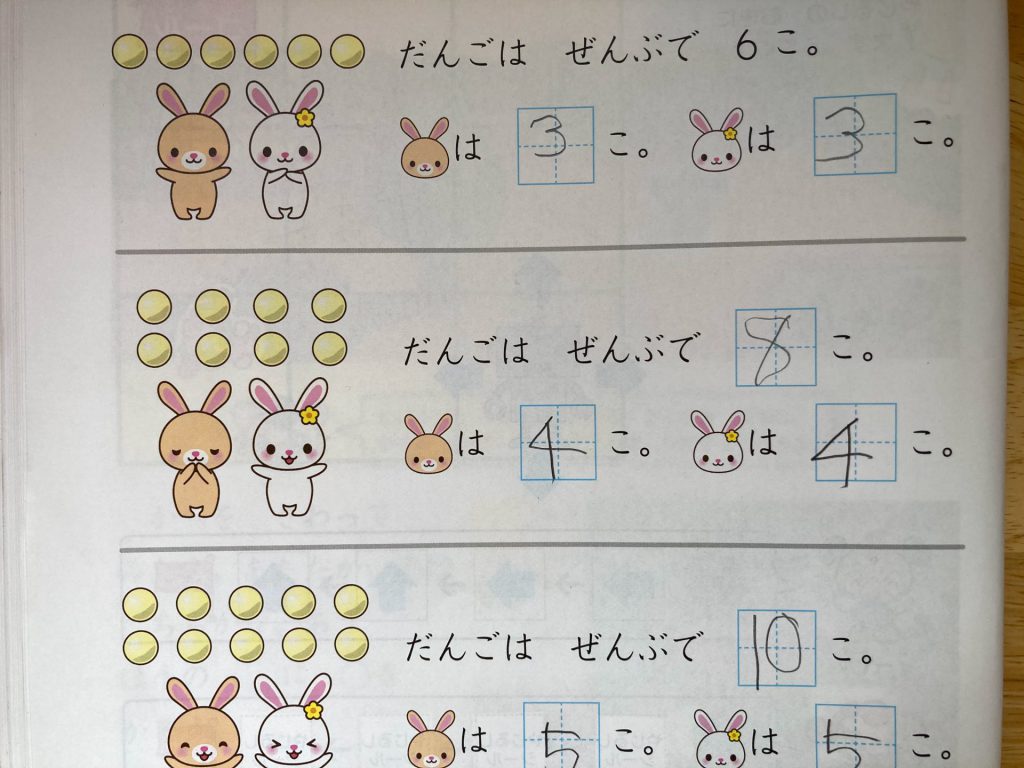
数字そのものは正解でしたが、より重要なのはどのように考えたのか、ということです。
- 考え方1:○をすべて数える
- 考え方2:足し算(4+4など)で考える。ただし、分け方はいくつかあります。たとえば、上下(1行4列)の4個つずつにわける、左右(2行2列)の4個ずつにわける。
- 考え方3:掛け算(4×2など)で考える。 ただし、分け方はいくつかあります。たとえば、上下(1行4列)と4個つずつにわける、左右(2行2列)4こずつにわける。
どうやって考えたのかを確認したところ、年長息子は考え方2を使っていました。そろばん教室で玉を使って足し算・引き算を学習しているからだと思います。足し算で考えようとしたこと自体が学習して進歩している証拠だと思います。
結局、小学生になっても、中学生になっても、高校生にになっても、算数・数学はどのように考えたのか、その過程がもっとも重要なので、幼児期からその習慣を付けさせたいと思っています。
特に小学校の算数(中学受験組なら小3~4年生くらいまで、非受検なら小6まで)は丸暗記すれば正解にたどり着きますが、正解したことそのものよりも、適切な解釈のもとの正解かどうかのほうが重要ですから。
- ①適切な解釈による正解
- ②適切な解釈による不正解
- ③不適切な解釈による正解
- ④不適切な解釈による不正解
この4つのうちのどれに該当するのかは、本人から説明してもらわない限りわかりません。①と④なら特に問題ありませんが、注意しなければならないのは②と③です。最も注意すべきは③です。
②は不正解になって間違いとして表面化するので特に問題ありません。解釈そのものは適切なので、よく言う”おしい間違い”です。
③は正解になったままで放置されます。不適切な解釈ではそのうちどこかでほころびが出ます。よくあるのは、マル暗記による正解です。がんばって覚えただけの正解はすぐ忘れますし、何よりもそのうちおもしろくなくなります。
不適切な解釈による正解を早期発見して、適切な解釈に修正していくこともまた大事な指導です。
プロ家庭教師として小中高生や大学生に指導する際においても、私が気を付けている点です。


コメント